Details

Category: Конкурсы Российского научного фонда (РНФ)

Published: 14 December 2017

Hits: 7428

Аннотация проекта:

Участникам проекта удалось в последние годы получить приоритетные результаты по влиянию перекрестной и магнитной спиральностей на каскадные процессы в МГД-турбулентности, а также условий воздействия гидродинамической спиральности на динамику инерционного интервала в обычной гидродинамической турбулентности. Целью проекта в развитии и использовании общего подхода к учету эффектов спиральности в магнитогидродинамических и конвективных турбулентных течениях, дающего согласованные результаты теории, численного моделирования и эксперимента.

Индийская команда, имеющая хороший опыт прямого численного моделирования турбулентности и доступ к высокопроизводительным кластерам, берет на себя основную нагрузку по проведению прямых численных исследований турбулентных потоков проводящей и непроводящей жидкости. Обе команды имеют опыт работы с каскадными моделями турбулентности и используют этот опыт для исследования турбулентных систем в области управляющих параметров, не доступных ни численному, ни лабораторному моделированию. В этих режимах будут изучены процессы спектрального переноса энергии, спиральности и магнитной спиральности при различных видах возбуждения МГД-турбулентности, а также исследованы процессы диссипации кинетической и магнитной энергии в развитой однородной и изотропной МГД турбулентности.

В рамках проекта российской стороной будут выполнены экспериментальные исследования спиральных конвективных течений в покоящихся и вращающихся прозрачных жидкостях с различными числами Прандтля с привлечением современных методов измерений поля скорости, таких как PIV, StereoPIV, TomoPIV. Одновременно будут разрабатываться модели галактического и Солнечного динамо с учетом обнаруженных спиральных эффектов, и вестись разработка методов обработки и интерпретации астрофизических наблюдений с целью восстановления структуры генерируемых магнитных полей. Эти результаты будут использоваться для верификации полученных теоретических и численных положений, а также будут представлять собственную ценность.

Cхема задач:

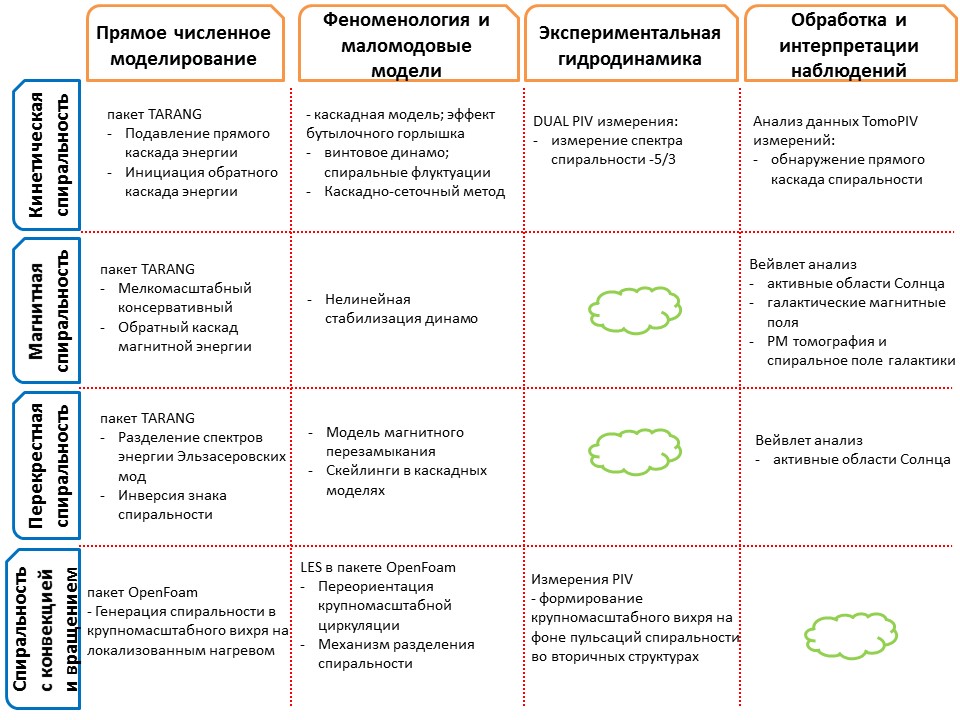
Основные участники российского коллектива:

Институт механики сплошных сред УрО РАН

Степанов Р.А. (рук.), Васильев А.Ю. (осн. исп.), Теймуразов А.С. (осн. исп.), Фрик П.Г. (осн. исп.), Сухановский А.Н. (осн. исп.), Титов В.В., Евграфова А.В., Попова Е.Н. 

Соколов Д.Д. (МГУ)

Основные участники зарубежного коллектива:

Верма Махендра Кумар (рук.)  профессор, физический департамент Индийского технологического института Канпура
Чакраборти Сагар, профессор ассистент, физический департамент Индийского технологического института Канпура
Франк Плуниан, профессор, Институт наук о Земле, Университета Гренобля
Самтаней Рави, профессор ассистент, Лаборатория вычислительной динамики жидкости и плазмы, Университет науки и технологии Короля Абдуллаха

Публикации (WoS):

1. K. Verma, R. Stapanov, F. Plunian , Energy transfers in MHD turbulence and its applications to dynamo // Magnetohydrodynamics, 2019 (accepted)
2. Titov, R.Stepanov, N. Yokoi, M. Verma, R. Samtaney, Cross helicity sign reversals in the dissipative scales of magnetohydrodynamic turbulence// Magnetohydrodynamics, 2019, (accepted)
3. Sokoloff, D.; Beck, R.; Chupin, A.; Frick, P.; Heald, G. & Stepanov, R. Combining Faraday tomography and wavelet analysis // Galaxies, 2018, V. 6, № 4,  121 10.3390/galaxies6040121
4. K. Verma, A. Kumar, P. Kumar, S. Barman, A. G. Chatterjee, R. Samtaney, R.A. Stepanov Energy Spectra and Fluxes in Dissipation Range of Turbulent and Laminar Flows // Fluid Dynamics, 2018, Vol. 53, No. 5, pp. 728–739. DOI: 10.1134/S0015462818050166
5. Stepanov R., Plunian F., Kinematic dynamo in a tetrahedron of Fourier modes // Fluid Dynamics Research, 2018, 50, 051409 DOI 10.1088/1873-7005/aab440 
6. Титов В., Степанов Р., Соколов Д. Магнитное поле в винтовом течении с флуктуациями //ЖЭТФ 2018, T.153. 4. C.566-572
   (Titov, V. V., Stepanov, R. A., Sokoloff, D. D. Magnetic Field in a Screw Flow with Fluctuations // Journal of Experimental and theoretical Physics 2018, V. 126, no. 4, P.566-572.) DOI 10.7868/S0044451018040041
7. Rodion Stepanov, Ephim Golbraikh, Peter Frick, Alexander Shestakov, Helical bottleneck effect in 3D homogeneous isotropic turbulence // Fluid Dynamics Research, 2018, 50, 011412 DOI: 10.1088/1873-7005/aa782e
8. Teimurazov A. S., Stepanov R. A., Verma M. K., Barman S., Kumar A., Sadhukhan S. Direct numerical simulation of homogeneous isotropic helical turbulence in the TARANG package // Journal of Applied Mechanics and Technical Physics, 2018, Vol. 59, No. 7, pp. 129–137 10.1134/S0021894418070131
9. Frick P., Stepanov R., Mizeva I., Inverse cascades in helically magnetized turbulence // Magnetohydrodynamics, 2017, 53 (1), p. 89-96
10. Sukhanovskii, A. Evgrafova, E. Popova, Helicity of Convective Flows from Localized Heat Source in a Rotating Layer // Archive of Mechanical Engineering, V. 64, N. 2, P. 177-188, 2017, DOI: 10.1515/meceng-2017-0011
11. Kalinin, D. D. Sokoloff, V. N. Tutubalin  The Intermittency of Vector Fields and Random-Number Generators // Moscow University Physics Bulletin, 2017, Vol. 72, No. 5, pp. 449–453. DOI: 10.3103/S0027134917050071
12. D. Sokolov, E. V. Yushkov, A. S. Lukin, Small-Scale Magnetic Helicity and Nonlinear Stabilization of the Dynamo // Geomagnetism and Aeronomy, 2017, Vol. 57, No. 7, pp. 1–5. DOI: 10.1134/S0016793217070192
13. L. Moss, D. D. Sokoloff, Parity Fluctuations in Stellar Dynamos // Astronomy Reports, 2017, Vol. 61, No. 10, pp. 878–882 DOI: 10.1134/S1063772917100079
14. Manohar K. Sharma, Mahendra K. Verma, and Sagar Chakraborty On the energy spectrum of rapidly rotating forced turbulence, Physics of Fluids 2018 30:11
15. K. Sharma, A. Kumar, M. K. Verma, and S. Chakraborty, Statistical features of rapidly rotating decaying turbulence: Enstrophy and energy spectra and coherent structures, Physics of Fluids, 30, 045103 (2018).
16. Bhattacharya, A. Pandey, A. Kumar and M. K. Verma, Complexity of viscous dissipation in turbulent thermal convection, Physics of Fluids, 30, 031702 (2018).
17. Kumar and M. K. Verma, Amplification of large-scale magnetic field in nonhelical magnetohydrodynamics, Phys. Plasmas, 24, 092301 (2017).
18. K. Verma, Physics of Buoyant Flows: From Instabilities to Turbulence, World Scientific (2018).
19. Sukhanovskii ,  Batalov  V., Stepanov R., Using of direct imaging and IPI techniques for measurements in nozzle sprays // AIP Conference Proceedings, 2016, 1770,  030023 DOI: 10.1063/1.4963965
20. Sukhanovskii A., Evgrafova A., Popova E., Non- zero helicity of a cyclonic vortex over localized heat source // Journal of Physics: Conference Series, 2016, 754 (7), 072005 DOI: 10.1088/1742-6596/754/7/072005
21. Stepanov R., Plunian F., Kinematic dynamo in a tetrahedron composed of helical Fourier modes // IOP Conference Series: Materials Science and Engineering, 2017, 208 (1), 012038 DOI: 10.1088/1757-899X/208/1/012038
22. Vasiliev A., Sukhanovskii A., Stepanov R., Numerical simulation of helical flow in a cylindrical channel // IOP Conference Series: Materials Science and Engineering, 2017, 208 (1), 012011 DOI: 10.1088/1757-899X/208/1/01201
23. Teimurazov A., Sukhanovskii A., Evgrafova A., Stepanov R., Helicity sources in a rotating convection // Journal of Physics: Conference Series, 2017, 899 (2), 022017 DOI: 10.1088/1742-6596/899/2/022017
24. Stepanov, P. Frick, V. Dulin, D. Markovich Analysis of mean and fluctuating helicity measured by TomoPIV in swirling jet // EPJ Web of Conferences, 2018 V. 180 P. 02097 10.1051/epjconf/201817002097
25. Rodion Stepanov, Andrei Teimurazov, Valerij Titov, Mahendra Verma, Satyajit Barman, Abhishek Kumar and Franck Plunian, Direct numerical simulation of helical magnetohydrodynamic turbulence with Tarang code // Proceedings of Ivannikov ISPRAS Open Conference, IEEE Xplore, 2017, 90-96 DOI 10.1109/ISPRAS.2017.00022
26. Р. А. Степанов, Д. Д. Соколов, Магнитная спиральность и перспективы её наблюдения в межзвёздной среде // УФН, принято в печать DOI: 10.3367/UFNr.2018.12.038503

Отправлено в журнал

• Vasiliev, P. Frick, A. Kumar, R. Stepanov, A. Sukhanovskii, M. K. Verma Transient flows and reorientations of large-scale convection in a cubic cell // Physical Review E
• Plunian, R. Stepanov, M. K. Verma, On nonuniqueness of transfer rates in hydrodynamic and MHD turbulence // J. Plasma Phys.
• Stepanov, P. Frick, V. Dulin, D. Markovich, Mean and fluctuating helicity in swirling jet flows // PRL

 Описание выполненных в 2018 году работ и полученных научных результатов: 

Основным содержанием теоретической части работ в 2018 было проведение масштабных численных экспериментов с использование прямого численного моделирования. Предварительно было проведено обобщение полученных совместно с индийской стороной специальных источников возбуждения турбулентных течений различной природы с акцентом на эффекты спиральности. Проведена классификация ранее использованных способов подкачки по характеру поведения во времени, распределению по масштабам и типу спиральности. Полученная методика была использована для создания новых модулей пакета TARANG, которые прошли тщательное тестирование и для сравнения новых результатов с ранее полученными результатами.
Одним из значимых научных результатов, который обобщает работы по нескольким направлениям, является разработанная математическая модель турбулентных течений со спиральностью различной природы. Основная новизна состоит в предложенных подходах к возбуждению спиральной турбулентности различной по характеру поведения во времени, распределению по масштабам и типу спиральности. В результате нами создано соответствующее расширение программного пакета TARANG, которое позволяет проводить численное моделирование широкого спектра проблем. Собран значительный материал путем сквозного перебора различных параметров модели, накрывающего весь заявленный проектом спектр проблем. Данный материал является нашим заделом для будущего анализа, который может быть проведен после окончания проекта. Также часть уже использованных нами данных будет в открытом доступе и может послужить для публикаций других исследователей на сетевом ресурсе TurbulenceHUB http://turbulencehub.org/. В этом случае ссылка на данный проект РНФ будет обязательным условием.
Можно выделить два конкретных результата, полученных с использованием пакета TARANG:
1) Получены спектральные распределения энергии и спиральности, свидетельствующие о проявлении эффекта подавления прямого каскада и инициации обратного каскада в гидродинамической турбулентности под действием распределенного источника спиральности. С помощью нового форсинга удалось преодолеть недостатки пионерских исследований в этом направлении. Инновационная составляющая представляет собой динамическое ("мягкое") насыщение подкачки спиральности. Было обнаружено, что полученное спиральное течение на крупном масштабе, несмотря на турбулентный характер форсинга, имеет вид отдельных когерентных структур близких к течениям Бельтрами. Это новый эффект представляет особый интерес в контексте проблемы динамо. 
2) Получены спектральные распределения кинетической энергии и магнитной энергии и перекрестной спиральности в задаче о МГД турбулентности с источником перекрестной спиральности. Во-первых, мы подтвердили эффект перекрестной спиральности, который ранее предсказывался на основе каскадных моделей. Теперь нами показано, что это справедливо и для турбулентности, описываемой полными уравнениями МГД турбулентности. Во-вторых, мы выявили, что за укручение спектра отвечает изменение спектрального распределения энергии одной из двух мод в переменных Эльзассера. В-третьих, обнаружен принципиально новый и неожиданный эффект инверсии перекрёстной спиральности в диссипативном диапазоне масштабов. Данному эффекту дано объяснение на основе модели магнитного перезамыкания.  Данная область исследований имеет очень большое применение в задачах о корональных выбросах Солнца, солнечном ветре, магнитных бурях и орбитальной погоде. 
Кратко перечислим наиболее значимые проведенные исследования и результаты:
1)	Предложена новая модель спиральной МГД конвективной магнитогидродинамической турбулентности с учетом вращения. Выведены все существующие законы сохранения передачи энергии и спиральностей, поля скорости, температуры и магнитного поля. Аналитически выделены источники, обусловленные вращением, силой плавучести и средней стратификацией и имеющие спиральную природу. Конкретно впервые было получено, что коррелированные пульсации температуры и скорости могут служить распределенным источником кинетической спиральности и усиливать эффект динамо. Опосредованно также наблюдается рост магнитной спиральности.  При включении вращения этот механизм значительно усиливается в крупномасштабной части спектра.
2)	По результатам прямого численного моделирования на сетках с размерами до 4096 в кубе проведена валидация двух известных моделей турбулентности, позволяющих описать энергетические и спиральные спектры в инерциальном и диссипативном интервалах одновременно. 
3)	В результате разработки новых подходов к анализу спиральности космических магнитных полей по наблюдательным данным был предложен новый метод, основанный на вейвлет преобразовании. Разрабатываемые модели галактического динамо позволили получить модель магнитного поля спиральной галактики, которая послужила решающим результатом для обоснования нового и перспективного метода томографии по данным фарадеевских мер вращения галактики NGC 6946. 
4)	Также мы модифицировали метод обнаружения магнитной спиральности в магнитных полях галактик, который в настоящий момент вселяет наибольшие надежды. Работоспособность метода показана на реальных данных длинноволновых измерений радиотелескопа LOFAR на участке неба 5x5 градусов в  направлении галактики IC 342.

Впервые, при помощи оригинального подхода, предложенного участниками проекта, на основе измерений полей скорости методом dualPIV было восстановлено распределение компонентов спиральности. Теоретически было показано, что спектр спиральности может быть определен по измерениям в одной плоскости только при условии изотропности поля скорости. В общем случае закрученной струи это не выполняется. Поэтому была рассмотрена менее строгая гипотеза об осевой симметрии статистических свойств турбулентности. Для этого корреляционный тензор был разделен на полоидальную и тороидальную составляющие. При таком разложении необходимы измерения в двух несоосных (не проходящих через одну ось вращения) плоскостях. Получены распределения компонент спиральности в зависимости от высоты, то есть по ходу развития свободной закрученной струи, для различных скоростей течения на входе в дивертор. На полученных распределениях спиральности было показано наличие совместного прямого каскада энергии и спиральности со степенным законом близким -5/3 в диапазоне волновых чисел от 1 то 50. По результатам подготовлена статья.

Проведено экспериментальное изучение формирования спиральных конвективных течений во вращающемся слое с локализованным нагревом. Значимость этих исследований обусловлена тем, что, во-первых, конвекция может служить источником спиральности и, во-вторых, течение во вращающемся слое с неоднородным нагревом характеризуется неоднородным распределением спиральности. При помощи лабораторных экспериментов были  проведены измерения полей скорости для широкого интервала параметров и определены режимы для прямого численного моделирования. При помощи модернизированной установки удалось достичь развитых турбулентных режимов (Ra~10^9), в которых энергия пульсаций течения была сравнима или превосходила энергию среднего (по времени) течения. Были восстановлены поля скорости, завихренности, пульсаций различных компонент скорости, энергии пульсаций течения и среднего течения. В рассматриваемой системе вихри формируются за счет восходящих конвективных струй, поэтому области с высокими значениями завихренности являются индикаторами областей с высокими значениями спиральности.  Показано, что в развитых турбулентных режимах не происходит формирования устойчивого, расположенного в центральной части конвективного вихря. Вместо этого наблюдается образование нестационарных, вихрей большой интенсивности. Обнаружены режимы, в которых вместо одного локализованного вихря формируется пара интенсивных, вытянутых по вертикали вихрей (вихревые жгуты).  Изучение этих структур при помощи прямого численного моделирования представляет несомненный интерес.

Проведено теоретическое исследование динамики крупномасштабной конвективной циркуляции в кубической полости. Проблема стохастических реориентаций крупномасштабной циркуляции (КМЦ) в замкнутых полостях, помимо большого фундаментального и прикладного значения, непосредственно связана с задачами проекта, а именно с формированием и переносом спиральности в конвективной турбулентной среде.  Были проведены долговременные численные расчеты турбулентной конвекции в кубе в трехмерной постановке. Впервые для анализа динамики КМЦ были использованы интегральные характеристики (компоненты полного углового момента). Впервые было обнаружено спонтанное формирование азимутальных течений с ненулевым угловым моментом в турбулентной конвективной среде в неподвижной полости. Этот результат очень важен для различных геофизических процессов. Одним из наиболее острых вопросов является связь между средним азимутальным течением и реориентациями КМЦ. На основе корреляционного анализа было показано, что вращение плоскости КМЦ и среднее вращение жидкости коррелируют только частично, при этом большинство спонтанно формирующихся азимутальных течений не приводят к реориентации КМЦ. При этом было обнаружена высокая корреляция между высокочастотными осцилляциями компонентов интегрального углового момента (с фазовым сдвигом) и осцилляциями КМЦ в области диагонали. Разработан новый подход, описывающий процесс реориентаций. Вместо представления КМЦ в виде одного крупномасштабного вала мы рассматриваем КМЦ как суперпозицию двух ортогональных крупномасштабных квазидвумерных валов. В представленном подходе процесс реориентации обусловлен разрушением одного из квазидвумерных валов. Показано, что на фоне КМЦ возникают вторичные валы меньшего масштаба, располагающиеся вдоль ребер куба. Впервые было показано, что валы являются спиральными и знак спиральности определяется их расположением относительно плоскости КМЦ. Таким образом, обнаружен механизм разделения вторичных вихрей по знаку их спиральности в условия глобального вращения и стратификации. Данный результат важен для понимания механизмов Солнечного динамо.

 Описание выполненных в 2017 году работ и полученных научных результатов:

Работа по проекту в 2017 году включала теоретический анализ, численное моделирование и эксперимент и полностью следовала  заявленной методологии достижения целей проекта, а именно согласованное продвижение по 4 крупным направлениям: 
- методы и подходы прямого численного моделирования 
- методы эмпирических и полуэмпирических подходов к описанию мелкомасштабного поля на уровне средних полей.
- экспериментальная гидродинамика, оптические методы измерений.-
- методы обработки и интерпретации наблюдений.
Центральным местом развиваемой теории спиральных течений является определение взаимосвязи спектральных распределений энергии и спиральностей различного типа с их спектральными потоками, возникающими под действием различных источников. Такая постановка позволила впервые дать качественно и количественное объяснение как ранее известным, так и новым теоретически предсказываемым эффектам спиральности. Кратко перечислим основные особенности полученных нами эффектов:
1)	Эффект кинетический спиральности, который приводит к ослаблению прямого каскада в масштабах с высоким уровнем относительной спиральности. Результатом проведенных вычислительных экспериментов стало установление связи между уровнем  относительной спиральности и энергией, удерживаемой спиральностью, в этом масштабе. Это позволяет предсказывать спектральное распределение в мелких масштабах. В присутствие распределенного источника спиральности в крупных масштабах мы ожидаем обратный каскад энергии и спиральности. При этом нами показана связь между интенсивностью подкачки спиральности и спектральным потоком энергии от масштаба ее подкачки к крупным масштабам системы. В МГД течениях мы обнаруживаем, что нарушение баланса между спиральными модами является необходимым условием эффекта динамо. Основная линия, которую нам удается проводить, заключается в признании того факта, что критическим является именно условие нарушение баланса между спиральными модами, а не какая-то конкретная интегральная спиральная характеристика. Это может быть обычная спиральность, а может быть потенциальная. Масштаб системы, где этот баланс нарушается, инициирует динамо процесс (как мелкомасштабного, так  и крупномасштабного динамо). Для случая конвективной турбулентности результатом является обнаружение механизма реализации спектра Обухова-Болджиано. 
2)	Эффект магнитной спиральности качественно схож с эффектом кинетической спиральности, но как было показано, принципиально отличается по механизму действия и по связи интенсивности источника и потока магнитной энергии, вызываемым эффектом спиральности.  В первую очередь это вклад мелкомасштабных структур в динамику крупномасштабных структур.
3)	Эффект перекрестной спиральности сводится к блокировке мелкомасштабного динамо и ослаблению совместного каскада кинетической и магнитной энергии. Каскад перекрестной спиральности может быть в равной степени как прямым, так и обратным, что определяется исключительно направлением каскада кинетической и магнитной энергий.
Мы получили ряд важных практических результатов:
- в задаче о винтовом динамо показано различие решения уравнения среднего поля и решения на основе прямого численного моделирования при конечном времени корреляции. Установлено, что флуктуации со спиральностью того же знака, что и спиральность среднего течения не влияют на динамо механизм, в то время как противоположные по знаку - существенно замедляют рост магнитного поля (статья отправлена в журнал).
-создана численная и программная реализация каскадно-сеточного метода с применением параллельных вычислений. Каскадно-сеточный метод реализован в коде написанном на С++ с применением MPI для обеспечения работы в режиме параллельных вычислений. Использована одномерная блочная декомпозиция с адаптивной областью перекрытия соседних блоков. Причем обмен происходит только между значениями сеточных переменных, расчет по цепочке каскадных переменных идет независимо для каждого узла сетки.
- результат расчета подтвердил исходную гипотезу – действительно,  учитывая баланс спиральности, мы приходим к моделям с ярко выраженными резонансами. Вполне вероятно, что  именно такого рода явления приводят к реально  наблюдаемым ярким явлениям в динамике солнечной активности типа минимума Маундера.
- по результатам изучения свойств генерации слабого магнитного поля в зеркально-симметричной конвекции, выясняется, что ожидается значительный приток магнитной спиральности, сосредоточенной вблизи диссипативного масштаба магнитного поля в системе. Это говорит о возможности пересмотра сценария, описывающего нелинейное насыщение крупномасштабного динамо, основанного на идее сохранения магнитной спиральности. 
- впервые представлено прямое экспериментальное свидетельство каскада турбулентной спиральности от больших масштабов до малых масштабов. Получены распределения средних и флуктуирующих компонент спиральности, которое выявляют анизотропную структуру спирального струйного потока. Мы показали, что сценарий генерации и распада спирали вдоль струи существенно зависит от вихревого потока. Данный результат открывает прямой путь к верификации широко используемых моделей турбулентности и замыкания. 
- разработан метод вейвлет-анализа, предназначенный для спектрального и пространственного распределения токовой спиральности в активной области солнечного пятна. Метод протестирован на синтетических распределениях, полученных ранее предложенной оригинальной методикой. Предложен подход анализа пространственного распределения токовой спиральности на различных масштабах. Проведено сравнение полученных вейвлет-спектров со спектрами, полученными другими авторами с использованием преобразования Фурье.
- разработан генератор случайных чисел на основе спиральных каскадных моделей.  По сравнению с генераторами на основе эволюции других стохастических систем, каскадные модели (особенно спиральные) дают более естественную перемежаемость и тем самым более равномерную статистику высших моментов.

Экспериментальные работы второго года выполнения проекта были направлены на отработку метода dualPIV и изучение спиральных течений в различных физических системах:
1. Большие усилия были затрачены на реализацию метода dualPIV для изучения спиральной изотерической свободной струи воздуха за дивертором.   По результатам двумерных измерений в вертикальных и горизонтальных сечениях восстановлено среднее поле скорости в объеме и спиральность среднего течения. Проведено сравнение распределения спиральности среднего течения для свободной закрученной струи в эксперименте и закрученной струи в численном расчете. Была проведена модернизация и настройка системы PIV для реализации метода dualPIV. Проведены тестовые измерения методом dualPIV в незакрученной струе воздуха. Показано, что средние и пульсационные характеристики в плоскостях равноудаленных от центральной оси струи хорошо согласуются.  Проведена первая серия измерений методом dualPIV в спиральной струе. Проведено сравнение с результатами двумерных измерений методом PIV. На основе мгновенных полей скорости в параллельных плоскостях были восстановлены полевые характеристики спиральности. Разработанную и апробированную методику измерения спиральности планируется представить на международном симпозиуме по оптическим методам в гидродинамике. Наряду с экспериментальными измерениями были продолжены численные исследования эволюции спиральной струи при помощи математической модели. Было показано, что азимутальный вклад спиральности является отрицательным вблизи твердой стенки, а в центральной части канала, вблизи оси он положителен. Анализ несимметричной части течения показал, что она характеризуется большими значениями вблизи дивертора, но быстро спадает по мере удаления от дивертора и ее вклад становится пренебрежимо малым.  Зависимости интегральных значений азимутального и продольного вкладов спиральности от расстояния вдоль оси канала подобны, что является нетривиальным результатом. Показано, что течение за дивертором характеризуется большими значениями спиральности, сосредоточенными в наибольшем масштабе, и может использоваться в качестве генератора спиральности.  Обнаружено, что осесимметризация течения и быстрое затухание радиальной скорости позволяет использовать для оценки спиральности только радиальное распределение азимутальной и аксиальное компонент скорости. Этот результат представляется очень важным, так как позволяет использовать метод StereoPIV (измерение трех компонент скорости в плоскости) для мгновенных измерений спиральности в каналах.
2. Другим ключевым блоком экспериментальной части проекта является изучение конвективных течений от локализованного источника тепла во вращающемся слое. Наибольший интерес представляет реализация спиральных конвективных течений в развитом турбулентном режиме. В ходе второго года проекта были проведены измерения полей скорости в выделенных горизонтальных сечениях вплоть до значений чисел Рэлея Ra=107. Для реализации режимов с более высокими значениями чисел Рэлея был изготовлен новый нагреватель, вмонтированный в фальш-дно из термостойкого текстолита, что позволит существенно повысить допустимую температуру нагревателя. Для минимизации влияния боковых стенок на характеристики и структуру течения была подготовлена модель с большим аспектным отношением (отношение диаметра кюветы к диаметру нагревателя) а=7 (ранее использовалась модель с a=3). Совместно с проведением экспериментальных измерений в турбулентных конвективных течениях (для умеренных числе Рэлея) от  локализованного источника тепла во вращающемся слое было проведено прямое численное моделирование (DNS). Было проведено сравнение расчетных и экспериментальных данных для двух принципиально отличных режимов течения, в одном из которых циклонический конвективный вихрь устойчив, и находится в центре, а во втором вихрь непериодическим образом разрушается и формируется вновь на некотором расстоянии от оси вращения модели. Расчеты для обоих режимов показали хорошее согласие с экспериментальными данными. Были получены распределения спиральности, ее вкладов для описанных режимов. В случае неустойчивого вихря спиральность распределена в значительно большей области нижней части слоя.  Важным результатом является то, что спиральность в рассматриваемой системе характеризуется высоким уровнем пульсаций, что представляет особый интерес, именно пульсационная часть спиральности может принципиально влиять на динамику турбулентных течений. Для более глубокого понимания того, что является стоками и источниками спиральности был проведен анализ уравнения баланса спиральности. Показано, что временные вариации вязкого и конвективного членов уравнения значительно превышают изменения других членов уравнения и производной спиральности по времени. Показано, что конвективный член служит источником спиральности, а вязкий член напротив приводит к стоку большей части спиральности произведенной конвективным членом. Этот результат представляется чрезвычайно интересным и заслуживает отдельного исследования. 

 Описание выполненных в 2016 году работ и полученных научных результатов:

На первый год планировались работы, имеющие в основном подготовительный, тестовый и проектировочный характер. Были проведены все запланированные работы: разработка и отладка новых модулей пакета прямого численного моделирования Tarang, демонстрационные расчетов на различных сетках, получены эффекты спиральности в различных каскадных моделях турбулентности, подготовлены данные астрофизических наблюдений для анализа спиральности в МГД турбулентности, спроектированы и частично изготовлены экспериментальные установки, апробированы методы оптических измерений.

Основные результаты теоретических и численных работ состоят в освоении, обновлении, проверки работоспособности и эффективности программных кодов для проведения прямого численного моделирования турбулентных течений и расчетов турбулентных каскадов с помощью каскадных моделей, а также в проведении тестовых расчетов, подтверждающих проявления эффектов спиральности в турбулентных потоках различной природы.

Существенно расширены возможности пакета программ Tarang в плане выбора источников возбуждения турбулентного течения. Самый общий вид решаемой проблемы в рамках кода Tarang представляет собой магнетоконвективную задачу. Турбулентный поток может возбуждаться внешними массовыми силами, силой Кориолиса при наличии общего вращения системы, а также градиентом температуры, наложенным в одном направлении. На выбор имеются вариант детерминированной силы, обеспечивающий подкачку с постоянным притоком энергии и вариант случайной силы, обеспечивающий приток необходимых величин в среднем. Вносимые изменения документируются на сайте https://turbulencehub.org/.

Задача о спектральных свойствах спиральной гидродинамической турбулентности является самой исследуемой проблемой в задачах турбулентности, где затрагиваются вопросы о влиянии спиральности, к примеру, на коэффициент эффективной турбулентной вязкости. Эту задачу можно рассматривать в качестве своеобразного бенчмарка (benchmark). С использованием наших кодов были получены спектры энергии и спиральности, а также спектральные потоки. Результаты сопоставлены с феноменологическими оценками известных теорий. В частности рассчитана константа Колмогорова, которая зависит от типа подкачки. В плане масштабируемости код зарекомендовал себя очень хорошо. На сетке 64^3 время расчета составляет 1.8*10^-5 сек приведенной на одно ядро, один шаг и один узел сетки, а на стеках 128^3 и 256^3 наблюдается некоторое замедление до 2*10^-5. На сетках 512^3 и 1024^3 код работает более эффективно – время счета снижается до 1.4*10^-5.

Изучение МГД турбулентности с высоким уровнем перекрестной спиральности имеет прямое отношение к исследованию свойств солнечного ветра, построению моделей взаимодействия с ионосферой Земли. На основе проведенных расчетов методом прямого численного моделирования и с использованием каскадных моделей получены спектры энергии и спиральностей, спектральные потоки энергии и спиральностей при наличии сильного спектрального потока перекрестной спиральности. Проведенный анализ на основе разделения поля скорости и магнитного поля по спиральным модам показал, что установленный ранее эффект роста крутизны спектра энергии объясняется нарушением баланса спектральных потоков спиральных мод с разным знаком спиральности. На этой основе сформулирована феноменологическая теория, где характеристика, контролирующая скейлинг (спектральный закон) определяется величиной 1-C, где C – нормированная перекрестная спиральность.

Влияние кинетической и магнитной спиральности может наблюдаться как на прямом, так и обратном каскаде энергии. Для исследования всех возможных эффектов необходимый вычислительный эксперимент должен разрешать в общем случае два инерционных интервала. На данном этапе выполнения проекта мы ограничились использованием каскадных моделей турбулентности. Получены новые результаты описывающие спектры и спектральные потоки в интервалах масштабов более крупных, чем масштаб подкачки энергии. Установлена зависимость величины обратного каскада энергии от интенсивности подкачки спиральности.

Экспериментальная часть проекта состоит из двух блоков, первый это формирование течения с ненулевой спиральностью, что является нетривиальной задачей и второй блок – измерение спиральности, что также представляет серьезную проблему. В течение первого года выполнения проекта разработан и изготовлен экспериментальный стенд для формирования и исследования спиральных течений. Рабочий объем представляет собой кубическую полость со стороной 100 см. Конструкция полости позволяет проводить измерения в различной постановке. Для формирования спиральной струи разработан и изготовлен блок генерации спирального течения, который позволяет создавать течение с высокой степенью корреляции между вертикальной компонентой скорости и завихренностью, что обеспечивает существенный уровень спиральности. Конструкция дивертора, состоящего из набора пластин (лопаток), расположенных под углом к набегающему потоку является ключевым элементом блока генерации спиральности. Для выбора оптимальной конструкции дивертора была подготовлена математическая модель и проведена серия расчетов. В качестве основных характеристик рассматривались три компоненты скорости и завихренности, локальная и интегральная спиральности. Показано, что предложенная, восьмилопастная конфигурация дивертора позволяет создать спиральный поток. Для изготовления элементов генератора спиральности использовался 3D принтер Picaso.
Второй тип экспериментальной установки для исследования спиральности основан на использовании локализованного источника тепла. Для формирования локализованного источника предложен оригинальный подход на базе индукционного нагревателя. Благодаря малой толщине диска и использованию индукционного нагрева предложенный тип нагревателя является малоинерционным и мощным. Качественные наблюдения показали, что локализованный нагрев формирует интенсивную восходящую конвективную струю. Однородность нагрева проверялась при помощи тепловизионной камеры и системы термопар. Для создания вихревого движения изготовлен набор пластин. Количество пластин и их ориентация под углом к набегающему радиальному течению позволяет регулировать интенсивность азимутальной компоненты  скорости. Изучение конвективных течений требует измерения температуры в различных областях модели. Для проведения температурных измерений была подготовлена автоматизированная система измерений температуры.

В связи с изучением влияния спиральности на формирование крупномасштабных атмосферных вихрей была проведена серия измерений на лабораторной модели тропического циклона. Получены распределения двух компонент скорости в различных горизонтальных сечениях. Восстановлены средние поля скорости в слое. Показано, что полученное течение обладает спиральностью определенного знака. Применяемая в экспериментах измерительная система не позволяла провести мгновенные измерения трех компонент скорости, поэтому совместно с экспериментом была проведена серия расчетов в CFD пакете FlowVision. Результаты расчетов и эксперимента хорошо согласуются. Анализ мгновенных трехмерных полей скорости полученных в расчетах показал, что спиральность в рассматриваемой системе определенного знака, а основной вклад вносит конвективное спиральное течение в центральной части. Обнаружено, что сдвиговое течение вблизи верхней границы на периферии также приводит к формированию области с ненулевой спиральностью. В целом показано, что рассматриваемая система очень перспективна для изучения спиральности и требует детального рассмотрения.