Проект РФФИ 19-41 590004. Руководитель Васильев А. Ю.

На первом этапе экспериментально исследована структура и динамика крупномасштабной циркуляции в турбулентной конвекции Рэлея-Бенара для жидкостей с умеренными и высокими числами Прандтля.  Экспериментальная установка представляет собой кубическую полость со стороной L=250 мм (см. рис.1). В качестве рабочих жидкостей выступала дистиллированная вода, 25 % водный раствор пропиленгликоля и чистый пропиленгликоль. Эксперименты проводились при средних температурах жидкости 50 и 25 ^oС (для воды) и 20 ^oС (для 25 % водного раствора пропиленгликоля и чистого пропиленгликоля), что соответствует средним числам Прандтля Pr=3.5, Pr=6.1 и Pr=64. Разложение двумерных полей скорости на фурье-моды показало, что при изменении числа Прандтля от 3.5 до 24 в течении доминирует одна крупномасштабная мода (см. рис. 1). При дальнейшем росте числа Прандтля структура течения существенно меняется и энергия распределяется между несколькими основными фурье-модами. Происходит также существенное изменение временной динамики доминирующей моды.

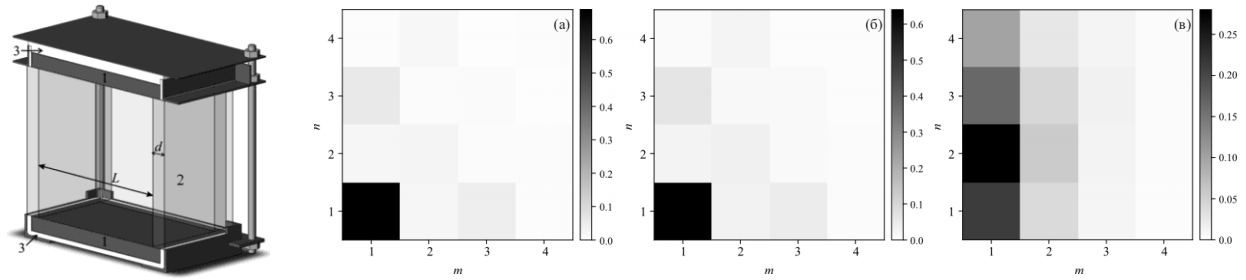
Рис.1 Экспериментальная установка в разрезе: 1 – медный теплообменник, 2 – плексигласовые боковые стенки толщиной d=25 мм, 3 – теплоизолятор. Нормированная энергия фурье-мод: (а) – Pr=6.1, Ra=2.0·10⁹, (б) - Pr=24, Ra=1.3·10⁹, (в) - Pr=64, Ra=1.3·10⁹

Большое внимание было уделено численному моделированию конвективной турбулентности с неоднородным нагревом при умеренных и высоких числах Рэлея (10^7<ra<2x10^9). Неоднородный нагрев создавался только на нижней границе кубической полости при помощи смешанных граничных условий (см. рис.2). На границе были выделены «проводящие» области, которые поддерживались при постоянной температуре, а оставшаяся часть границы считалась теплоизолированной, т.е. тепловой проток равен нулю. В расчетах рассматривались три конфигурации распределения нагреваемых областей: (I) - локализованный нагрев; (II) - девять нагревателей одинакового размера, равноудаленные друг от друга; (III) – комбинация из нагреваемых областей трех размеров с неоднородным распределением по пространству.

Обнаружено, что при Ra=10^7 эффективность переноса тепла сильно зависит от распределения нагреваемых областей на нижней границе. Максимальные отличия в числе Нуссельта достигают 20%. В более развитом режиме (Ra=1.1x10^9) отличия не превышают 5%, поскольку турбулентность эффективнее перемешивает среду. При неоднородном нагреве показатель степени в зависимости числа Нуссельта от числа Рэлея может принимать два значения: beta~2/7 для конфигураций (I) и (II); beta~1/3 для конфигурации (III) (см. рис.3).

Рис.2 Схема вычислительной области. Варианты распределения нагреваемых областей. Черным цветом отмечены нагреваемые области.

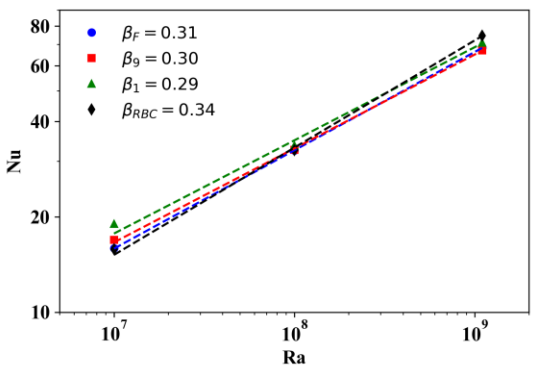
Рис.3 Зависимость числа Нуссельта от числа Релея в двойных логарифмических координатах, где индексами обозначено: 1 – локализованный нагрев, 9 – девять нагревательных областей, F – комбинация из нагреваемых областей трех размеров. Штриховые линии показывают степенные законы Nu~Ra^β.

Кроме того, исследовано влияние многомасштабного рельефа поверхности теплообменника на процессы переноса тепла в замкнутой полости. Задача решалась в сопряженной постановке. Нижний теплообменник представлял собой медную плиту толщиной 10 мм, на поверхности которой имеются выступающие прямоугольные элементы. Комбинация из элементов трех разных размеров в поперечном сечении формирует фрактальную топологию поверхности теплообменника. На рис.4 показаны распределения температуры в медном массиве и зависимости числа Нуссельта от числа Релея для двух высот рельефа.

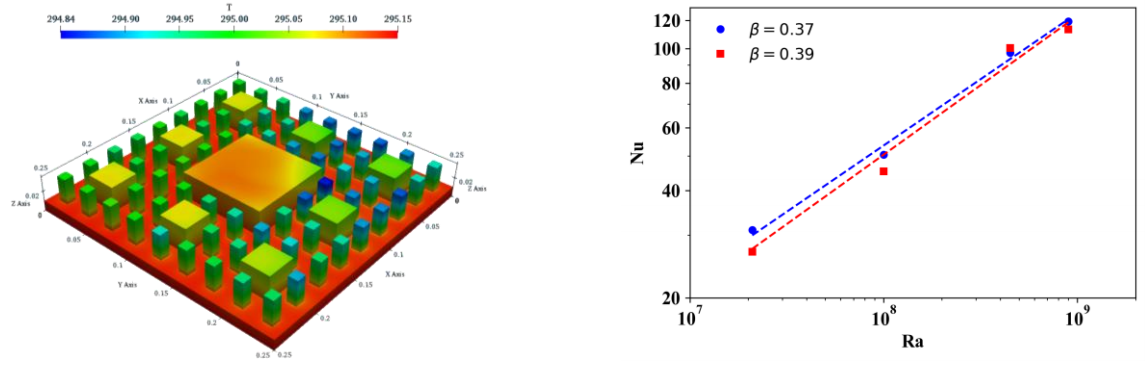
Рис.4 Левая панель – распределение температуры на поверхности теплообменника. Правая панель – зависимость числа Нуссельта от числа Релея в двойных логарифмических координатах: ● – h/L=0.1, ■ - h/L=0.05. Штриховые линии показывают степенные законы Nu~Ra^β.

II Этап (2020)

На втором этапе проекта было продолжено исследование влияния смешанных граничных условий на процессы теплообмена при помощи численного моделирования. Рассматривалась конфигурация, представляющая собой 225 нагреваемых областей одинакового размера, равноудаленных друг от друга. Результаты численного моделирования сравнивались с результатами следующих конфигураций нагрева: локализованный нагрев; девять нагревателей одинакового размера, равноудаленные друг от друга; комбинация из нагреваемых областей трех размеров с неоднородным распределением по пространству. Во всех конфигурациях площадь нагрева одинаковая и составляет 30% от площади верхней границы. Расчеты были выполнены для Pr=6.46 и Ra=10⁷. В случае с 225 нагревателями наблюдается наибольший конвективный тепловой поток – примерно 71% от случая с однородными граничными условиями. Тепловой поток со смешанными граничными условиями сильно неоднородный и определяется толщиной температурного пограничного слоя. Неоднородность температурного пограничного слоя (см. рис.1) является результатом нескольких факторов: структура крупномасштабной циркуляции и мелкомасштабные движения над нагреваемыми областями. Горизонтальный размер нагреваемых областей является ограничивающим фактором для толщины пограничного слоя, поэтому, чем меньше нагреваемая область, тем тоньше пограничный слой. Это означает, что тепловой поток увеличивается с уменьшением размеров нагреваемых областей. Толщина теплового пограничного слоя может быть меньше, чем для конвекции Рэлея – Бенара с однородными граничными условиями.

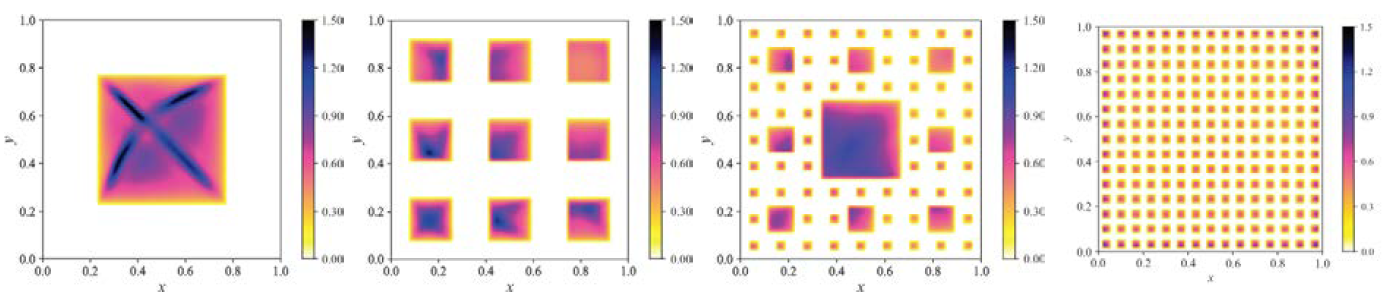
Рис.1. Осредненная по времени нормированная толщина температурного пограничного слоя δ^*= δ/δ₀, где δ₀ средняя толщина температурного пограничного слоя для конвекции Рэлея – Бенара с однородными граничными условиями.

Большое внимание было уделено экспериментальному исследованию влияния многомасштабного рельефа поверхности на процессы теплообмена в конвективной турбулентности. Эксперименты проводились в кубической полости с длиной ребра L=250 мм. В качестве рабочей жидкости выступала дистиллированная вода (Pr=6.12) и силиконовое масло ПМС-5 (Pr=62). Нижний теплообменник представлял собой медную плиту толщиной 10 мм, на поверхности которой имеются выступающие прямоугольные элементы. Комбинация из элементов трех разных размеров в поперечном сечении L/3, L/9, L/27, вытянутые на разную высоту h₁=10 мм, h₂=5 мм, h₃=2.5 мм, соответственно. В экспериментах относительное увеличение площади поверхности (отношение площади рельефной поверхности к площади верхней границы) составляет Cs=1.22. На рис.2 представлены зависимости числа Нуссельта от числа Рэлея. Эксперименты показали, что тепловой поток в случае рельефной поверхности всегда больше, чем для гладкой поверхности. Из рис. 2 (левая панель) видно, что число Нуссельта в случае Pr=62 приблизительно на 8% больше, чем для Pr=6.12 при одинаковых числах Рэлея. Однако с увеличением числа Рэлея эта разница уменьшается. Теория предсказывает степенной закон для зависимости числа Нуссельта от числа Рэлея Nu~Ra^β. Показатель степени β уменьшается с увеличением Pr: β=0.39 (Pr=6.12) и β ~1/3 (Pr=62). Обнаружено, что увеличение теплопереноса при Pr=6.12 меньше, по сравнению с относительным увеличением площади теплообмена из-за выступающих элементов (см. рис.2, правая панель). Ситуация существенно меняется при Pr=62. В этом случае наблюдается положительный эффект от использования многомасштабного рельефа поверхности, который заключается в усилении теплообмена по сравнению с относительным увеличением площади.

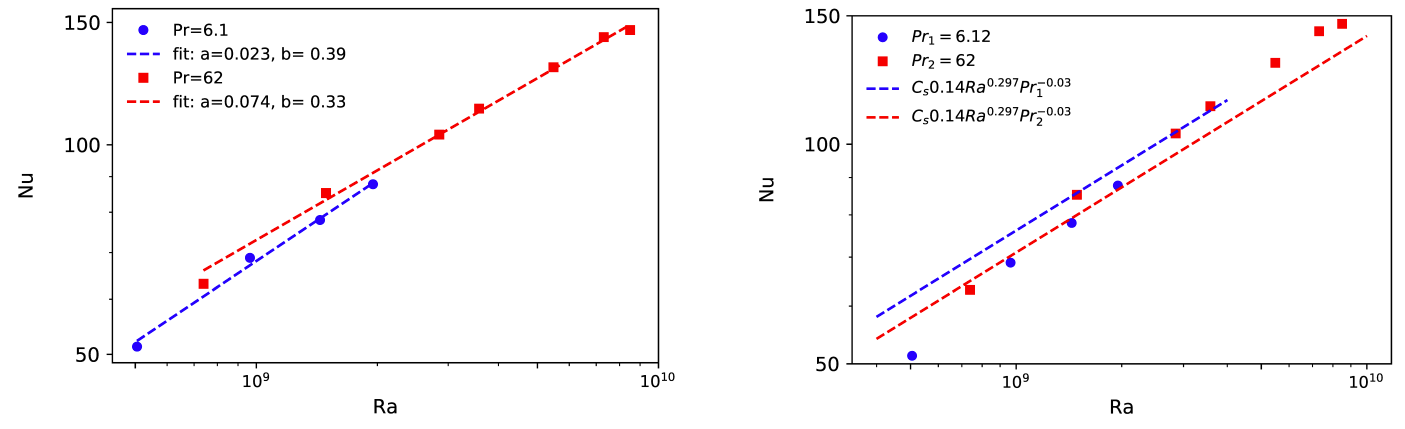
Рис.2 Зависимость числа Нуссельта от числа Рэлея в двойных логарифмических координатах. На правом графике пунктирные линии показывают увеличение теплового потока за счет дополнительной площади выступающих элементов: синяя линия – Pr=6.12, красная линия – Pr=62.

Кроме того, было выполнено численное моделирование конвективной турбулентности в случае с многомасштабным рельефом нижней границы. В расчетах рассматривались две конфигурации многомасштабного рельефа. Первая конфигурация (см. рис.3а) представляет собой комбинацию выступающих элементов прямоугольной формы с поперечными размерами L/3, L/9, L/27, вытянутые на разную высоту h₁/L=0.04, h₂/L=0.02, h₃/L=0.01, соответственно. Для данной конфигурации расчеты были выполнены для Pr=6.12, числа Рэлея варьировались от 10⁶ до 2×10⁹. Обнаружено два режима теплопередачи. Первый режим характеризуется β ~ 1/3 в интервале чисел Рэлея от 10⁶ до 2×10⁷. Второй режим наблюдается при больших числах Рэлея и характеризуется β ~ 0.40.
Вторая конфигурация рельефа представлена на рис.3б. Поперечный размер выступающих элементов одинаковый и равен L/27. Отношение высоты выступающих элементов к высоте кубической полости h/L варьируется от 0.04 до 0.01. Площадь рельефной поверхности в Cs=1.61 раз больше площади плоской верхней границы. В случае второй конфигурации расчеты были выполнены для Pr=6.12, и число Рэлея варьировалось от 10⁶ до 2×10⁷. В этом случае наблюдается только один режим, который характеризуется β~1/3. Числа Нуссельта имеют близкие значения для двух конфигураций рельефа. Наибольшее отличие в тепловых потоках составляет около 10% для Ra=1.13×10⁷.

Рис.3 (а, б) - конфигурации рельефа нижней границе. (с) - Зависимость числа Нуссельта от числа Релея в двойных логарифмических координатах: ● – первая конфигурация, ■ – вторая конфигурация. Штриховые линии показывают степенные законы Nu~Ra^β.

.

• Prev
• Next